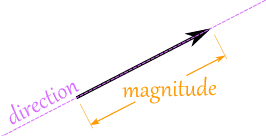
Un vector es un segmento que tiene orientación, dirección y magnitud.
El vector unitario es aquel que tiene una unidad de magnitud. Se representa el vector unitario con un gorrito en la letra.


Todo vector unitario puede ser escrito en términos del sen(t) y cos(t) que forma con el ángulo del eje x positivo.
OPERACIONES CON VECTORES
Suma de vectores
Se define el vector suma de ambos (w) a otro vector cuyas componentes se calculan sumando las componentes de cada uno de ellos.
El producto escalar de dos vectores u y v que forman un ángulo φ se define como:
De la expresión anterior se observa que el producto escalar de dos vectores no es un vector, es un número (un escalar). Además el producto escalar de dos vectores perpendiculares es nulo. Se deducen entonces los siguientes resultados:
Si los vectores están expresados en componentes, en tres dimensiones y aplicando los resultados anteriores se obtiene que:
El producto vectorial de dos vectores que forman un ángulo φ es otro vector, de dirección perpendicular al plano formado por los dos vectores, sentido el que da la regla de la mano derecha y módulo el que se especifica a continuación:
El producto vectorial no posee la propiedad conmutativa, ya que se cumple que:
Además, se cumple que el producto vectorial de dos vectores paralelos es nulo. Se obtienen entonces las siguientes relaciones:
Si los vectores vienen expresados en componentes el producto vectorial se calcula desarrollando el determinante.
|


No hay comentarios:
Publicar un comentario